プログラミング初心者の勉強日記

情報科学専攻です. 機械学習と競技プログラミングについて日々勉強しています.

勾配法

これなら分かる最適数学

「これなら分かる最適化数学」を読み始めたので、最適化についても紹介していこうと思います.

これなら分かる最適化数学―基礎原理から計算手法まで

これなら分かる最適化数学―基礎原理から計算手法まで

作者: 金谷健一
出版社/メーカー: 共立出版
発売日: 2005/09/01
メディア: 単行本
購入: 29人クリック: 424回
この商品を含むブログ (42件) を見る

関数の最適化の代表の手法の「勾配法」を軽く説明し、実装例を示そうと思います.

1. 勾配法
2. 勾配法の実装例
3. 勾配法の問題点

1. 勾配法

1変数の場合と多変数の場合があるので今回は1変数の場合を説明します.

そもそも最適化とは、ある制約条件のもとで関数の値を最大（最小）にする変数の値を求めることを言います. 勾配法のアルゴリズムは単純であるが昔からよく使われる手法の一つです.

まず初期値 $x_0$ を与えます. この初期値の与え方についても多くの研究がされているが今回は割愛します.

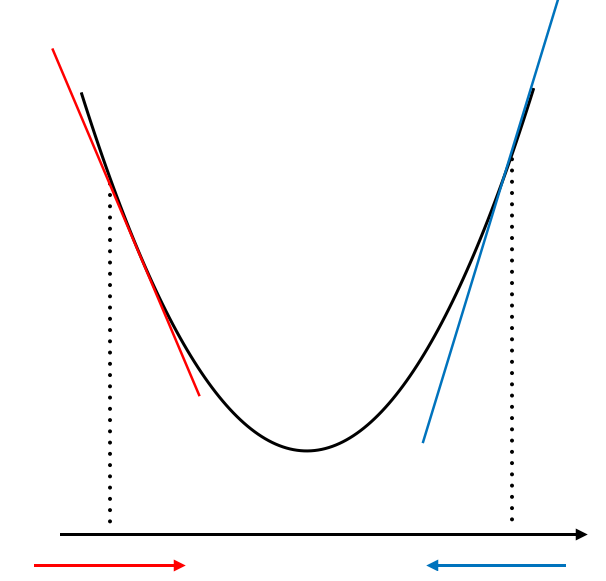
$f^{\prime}(x_0) = 0$ ならそこで最大(最小)値をとります. ある点での勾配が正、つまり $f^{\prime}(x_t ) > 0$ のとき(下図の青)はその点から負の方向に、勾配が負のとき、つまり $f^{\prime}(x_0)$ < 0のとき(下図の赤)はその点から正の方向に少し進むことで、目的地(最大、最小となる点)に近づいていきます. 簡単にまとめたアルゴリズムを以下に示します. f:id:linearml:20170903230043p:plain

xの初期値 $x^{0}$ を与える
もし $f^{\prime}(x^{0}) = 0$ のとき、そのときの $x_t$ が最大(最小)値をとる地点である
$x^{t} = x^{t-1} - \alpha f^{\prime}(x^{t-1})$ に更新する (ただし、 $\alpha$ は学習率と呼ばれ1ステップでどれだけ更新するかを表すハイパーパラメータである)
収束するまで2, 3を繰り返す

計算機で実装する上でちょうど $f^{\prime}(x)=0$ となるxを求めるのは現実的ではないので、ある小さい値 $\epsilon$ に対して、 $|f^{\prime}(x)|$ < $\epsilon$ になる点に到達した時に収束したとみなすことにします. また導関数は $\lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$ を用いて数値微分します.

2. 勾配法の実装例

以下にソースと結果を載せておきます.

f:id:linearml:20170903232812p:plain

初期値は $x=5$ で53回の繰り返しで収束しています. (オレンジの線が移動した経緯を示している.)

多変数の場合も基本的な流れは同じで各点での導関数を求め少しずつ動かしていけば良いですが今回は説明を省きます.

3. 勾配法の問題点

勾配法は単純で有効な手法であるが問題点もいくつかあります. 一つ目は初期値の与え方によって局所解に陥ってしまうことです.

二つ目は勾配を計算しなければならないが、微分できない関数であったり、できたとしても複雑すぎる場合があります.

また変数が数百、数千のときも勾配を求めるのが大変なことです.

なので色々な最適化の手法を知ることが必要であり、それぞれの関数に対して適切な手法を選ぶことが求められます.