プログラミング初心者の勉強日記

情報科学専攻です. 機械学習と競技プログラミングについて日々勉強しています.

MENU

論文を読むときにgoogle翻訳がいらなくなるwebサービス「transsay」を作ってみた

transsayとは

transsayは英語論文をコピペするだけで良い感じに翻訳してくれるwebサービスです。

Google翻訳があるからこんなのいらないじゃないかって？ そんなことありません！

Google翻訳にただコピペするだけでは、日本語訳が変になっているという経験はありませんか？

それは改行やハイフネーションがあるからなのです。

transsayを使って、サクサク論文を読んじゃいましょう。

はじめに

みなさん、英語論文を読むのは得意ですか？私は、苦手です。。。

B4や修士になったら嫌でも英語論文を読まなければなりませんよね。苦手だからやらないなんて言ってられません。

英語論文を読むのが苦手な方は、いつもどのように論文を読んでいますか？ 英語を得意になりたいからと何も調べずに自力で頑張る人もいれば、知らない単語を調べながら読む人もいると思います。

しかし、一番多いのは、Google翻訳などを使ってコピペする人が一番多いんじゃないでしょうか？ もちろん私も、章ごとにコピペして読んでコピペして読んでを繰り返していました。

しかし、論文をただコピペするとなんか変な日本語になったりしませんか？

それは文章の途中で改行が入っていたりハイフネーションがあったりすることが原因です (現在、Google翻訳ではハイフネーションをいれたままでもそのままいい感じに翻訳してくれています。さすが。 )。

そのままコピペすると？

例えば、この写真をみてください。 f:id:linearml:20190526191205p:plain

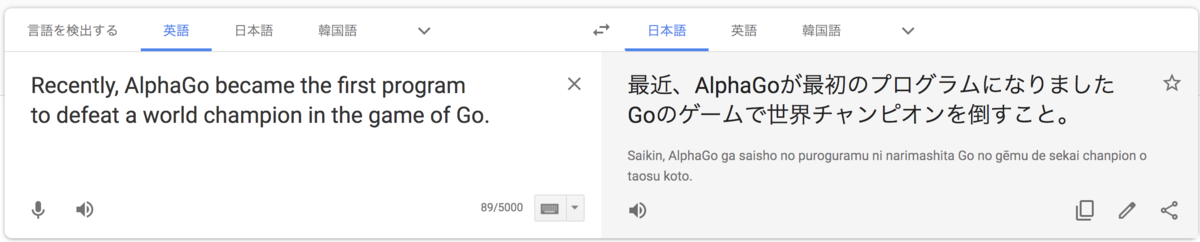
これは、alpha goを改良したalpha go zeroの論文である「Mastering the Game of Go without Human Knowledge」のアブストラクトの一部です。

論文をそのままコピペしただけだと、文の途中にある改行のせいで、正しく翻訳してくれていません。 (画像の例だと、programとtoの間に改行がある）

私は、この改行を手作業で消してからGoogle翻訳に投げていました。 本当に無駄な時間だったなあと思っています。

transsayが良い感じに翻訳してくれるよ

そこで、この改行があっても良い感じに翻訳してくれるwebサービス

transsay

を作りました。

「transsay」とは「translate + essay」に由来する造語で論文翻訳を意味します。

先ほどのGoogle翻訳に入力した文章と全く同じものを「transsay」に翻訳させてみます。 f:id:linearml:20190526191554p:plain

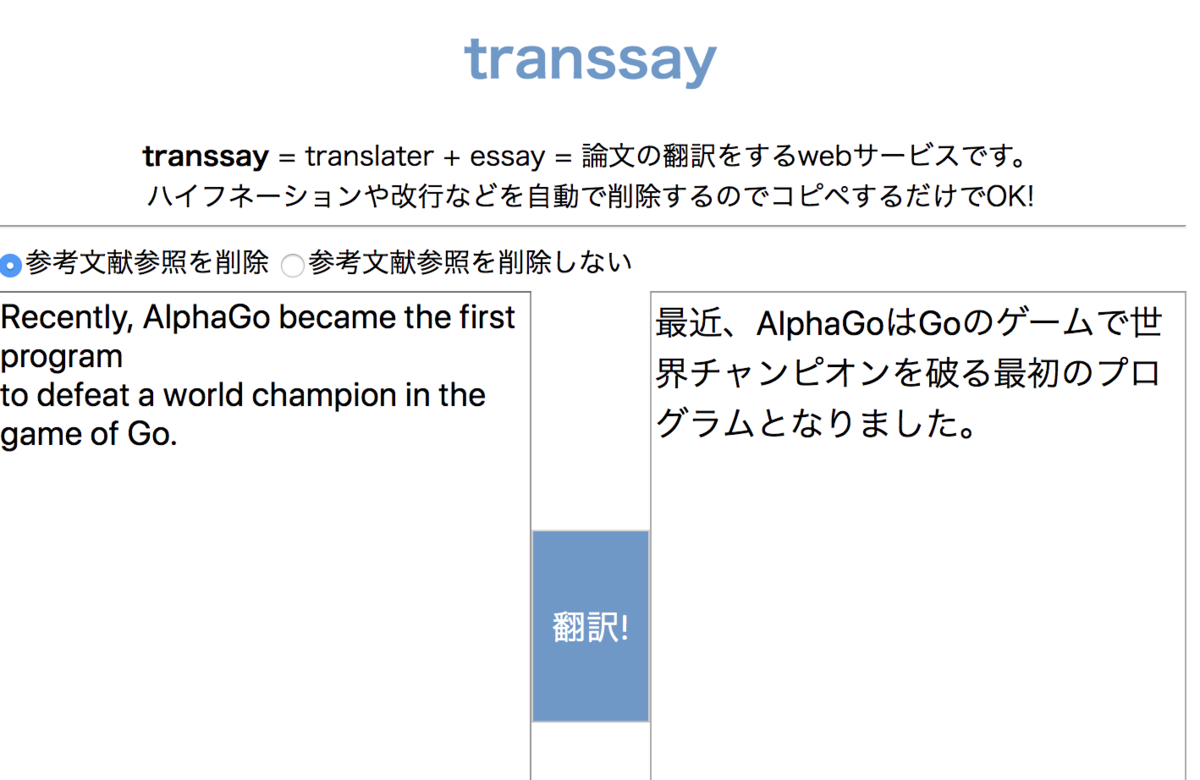
すると、改行を無視して、正しく翻訳してくれていることがわかります (囲碁を正しく翻訳できてないですけどね笑)。

まとめ

これで、手作業で改行を消すことなく、ただコピペするだけで英語論文を日本語で読めるようになります！ 是非transsayを使ってサーベイしまくってください！

CADDi 2018 for Beginnersに参加しました

競技プログラミング

CADDi 2018 for Beginnersに参加したので記録を残したいと思います.

今回のコンテストは、キャディ株式会社主催のABC/ARC形式のプログラミングコンテストで、レートが~1199までの人が参加できる初級者向けコンテストに参加しました。 要はいつものABC形式ですね。

問題のタイトルは以下のようになっています. 詳しい問題文は下のリンクから、公式のコンテストページでご確認ください.

A - 12/22

問題の概要

十進法表記でちょうど4桁の整数Nが与えられる. Nの十進法表記に何個の「２」が現れるかを求める.

解法

Nを文字列として受け取り、先頭から2があるかどうかをfor文で確認すれば良いです.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;
#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    string N;
    cin >> N;
    int rsl = 0;
    rep(i, 0, N.size()) {
        if(N[i] == '2') rsl++;
    }

    cout << rsl << endl;
}

B - AtCoder Alloy

問題の概要

長方形の板状の素材がN枚ある. i番目の素材の縦の長さ、横の長さはそれぞれA_i , B_iで与えられる. 縦の長さがH、横の長さがWの長方形の板を作りたい. 板を長方形の変に平行に切断することで、欲しい板を作ることができる素材はN枚中何枚あるかを求める. ただし、素材は向きが決まっているため回転することができない.

解法

i番目の素材を適切に切断することによって、縦の長さがH、横の長さがWの板を作ることができるとは、A_i \geq HかつB_i \geq Wを満たすときです. したがって、この条件を満たす素材の個数をカウントしてあげればよいことになります.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;

#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    int N, H, W;
    cin >> N >> H >> W;
    int A[N], B[N];
    rep(i, 0, N) cin >> A[i] >> B[i];

    int rsl = 0;
    rep(i, 0, N) {
        if(A[i] >= H and B[i] >= W) rsl++;
    }

    cout << rsl << endl;

}

C - Product and GCD

問題の概要

a_1, a_2, \cdots a_Nがある. a_1, a_2, \cdots a_Nの値はわからないが、a_1 \times a_2 \times \cdots \times a_N = Pはわかっている.

このとき、a_1, a_2, \cdots a_Nの最大公約数として考えられるもののうち、最大値を求める.

解法

N個の数列の積Pが与えられているので、Pを素因数分解します. 素因数分解した結果を、i番目の素因数をp_iとしたとき、

$$ P = p_1^{b_1} \times p_2^{b_2} \times \cdots \times p_m^{b_m} $$

と表せたとします. nがN個の数列の公約数になるのは、数列の各項が素因数の積でnを作れるときです. 最大公約数はそのうち最大のものなので、共通の素因数を全て使って掛け合わせたものになります.

例えば、20 = 2^{2} \times 5と8 = 2^{3}の最大公約数は共通の素因数2が2つなので、それらの積で表される、2 \times 2 = 4が最大公約数になります.

したがって、Pの各素因数を先頭から順にN個の数列の項に振り分けてあげれば良いことになります.

a_1 \times a_2 \times a_3 = 3240 = 2^{3} \times 3^{4} \times 5のとき、素因数2をa_1, a_2, a_3にそれぞれ一つずつ、3もそれぞれ1つずつ振り分けることができます. 5は1つしかなく、3つの項に振り分けることができません. したがって、a_1 = a_2 = a_3 = 2 \times 3 = 6を作ることができ、最大公約数は6になります. (残った素因数5を適当にa_1とかに振り分けても共通の素因数を他の項が持たないので最大公約数に影響を与えません.)

したがって、b_i \geq Nのとき、p_iを各項にb_i / N個振り分けていけば良いことになります.

素因数分解の部分は蟻本を参考にしました. 計算量は\mathcal{O}(\sqrt{n})なので、間に合います.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;

#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)

typedef long long ll;

map<ll, ll> prime_factor(ll n) {
    map<ll, ll> res;
    for(ll i = 2; i * i <= n; i++) {
        while(n % i == 0) {
            ++res[i];
            n /= i;
        }
    }
    if(n != 1) res[n] = 1;
    return res;
}

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    ll N, P;
    cin >> N >> P;

    map<ll, ll> m = prime_factor(P);
    
    ll rsl = 1;
    for(map<ll, ll>::iterator itr = m.begin(); itr != m.end(); itr++ ){
        if(itr->second >= N) rsl *= (pow(itr->first, itr->second / N));
    }
    cout << rsl << endl;

}

D - Harlequin

問題の概要

N色のりんごがあり、i番目の色のりんごはa_i個ある. このとき、先攻、後攻にわかれて以下の行動を交互に行う.

  • 1個以上のリンゴを選んで食べる. ただし、一度に選ぶリンゴは全て異なる色でなければならない.

最後のリンゴを食べた人を勝者とする. 先攻と後攻が最善を尽くすとき、どちらが勝つかを求める

解法

入力例1を例に考察してみます.

1番目のリンゴが1個、2番目のリンゴが2個あるとき、先攻は1番目のリンゴを1個食べれば、2番目のリンゴが2個残ります. このとき、後攻は2番目のリンゴを1個食べることしか選択肢がありません. 後攻が2番目のリンゴを一個食べた後は2番目のリンゴが1 個だけ残り、それを先攻が食べることで、先攻が勝利することができます.

毎ターン、各リンゴは最大でも1つしか減らないので、自分のターンにリンゴが奇数個ある場合、交互に1つずつ食べていくと最終的に自分が最後の一個を食べることができます. 逆に偶数個のときは、自分が最初にそのリンゴに手を出すと相手に最後の一個を食べられてしまいます.

1つでも奇数個のリンゴが存在すれば、そのリンゴだけを食べることで、全色のリンゴの個数を偶数個にすることができます. 全て偶数個になってしまったら、上で述べた理由から最後のリンゴを相手に食べられてしまうので、相手にその状況を作れた方が勝者となります.

したがって、各リンゴの個数のうち奇数のものが一つでも存在したら先攻が勝利します.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;

#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)

typedef long long ll;

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    int N;
    cin >> N;
    int a[N];
    int cnt_even = 0;
    rep(i, 0, N) {
        cin >> a[i];
        if(a[i] % 2 == 0) cnt_even++;
    }

    if(cnt_even == N) cout << "second" << endl;
    else cout << "first" << endl;

}

感想

パフォーマンス1600の順位26位という私にしては信じられないぐらいの結果でかなり嬉しいです.

C問題でWAを出さずにいたら1桁順位も狙え賞金をもらえたと思うと少し悔しいですが、久しぶりの全完で満足しています.

少し水色に近づいたので、これからも精進していき、一日でも早く「水色になるまでにやったこと」という記事をかけるように頑張っていきます.

オイラーのφ関数と競プロにおける例題

競技プログラミング

競技プログラミングでオイラーのφ関数を用いる問題を見つけたので、本記事では、オイラーのφ関数について軽く説明した後に、どのように用いたかの例を挙げます.

オイラーのφ関数

自然数nに対して、nと互いに素であるn以下の自然数の個数を\phi(n)で与えるとき、\phi(n)はオイラーの\phi関数 (ファイ関数) と呼ばれます. (オイラーのトーシェント関数とも呼ばれる.)

例えば、3と互いに素である3以下の自然数は、1と2の2つなので、\phi(3) = 2となります.

オイラーのφ関数の性質

  1. pが素数であるとき $$ \phi(p) = p - 1 $$ が成り立ちます. これは、1 \leq x \leq p - 1であるxに対して、pが素数なので、gcd(x, p) \neq 1となるxが存在しないことから容易に確認できます. ここで、gcd(x, p)はxとpの最大公約数を表します.

  2. 自然数kに対して、1 \leq x \leq p^{k}であるxの中にpの倍数であるものはp^{k - 1}個存在するので、pの倍数である個数を引いてあげらば良いことから、 $$ \phi(p^{k}) = p^{k} - p^{k - 1} = p^{k - 1}(p - 1) = p^{k}(1 - \frac{1}{p}) $$ が成り立ちます. (p^{1}, p^{2}, \cdots p^{k - 1}のk - 1個)

  3. gcd(m, n) = 1である自然数m, nに対して、 $$ \phi(mn) = \phi(m)\phi(n) $$ が成り立ちます.

オイラーのφ関数を用いる問題

オイラーのφ関数を用いる問題としてAOJのFarey Sequenceという問題がありました.

そもそもFarey Sequenceとはファレイ数列というもので初等整数論における興味深い性質をもつそうです. (この問題を解くまでファレイ数列の存在を知りませんでした...)

ファレイ数列とは、既約分数を順に並べた一群の数列であるとWikipediaに書いてありました.

もう少し具体的に言うと、一般項をF_nとしたとき、F_nとは、n以下の分母を持つ0以上1以下の全ての既約分数を小さな順から並べたものだそうです.

例えば $$ F_3 = (\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1}) $$ となりますし、 $$ F_4 = (\frac{0}{1}, \frac{1}{4}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{1}{1}) $$ となります.

AOJの問題では、nが与えられたときのF_nの個数を求めるという問題です.

上で挙げた、F_3とF_4に着目すると、F_4はF_3に\frac{1}{4}と\frac{3}{4}が加わっていることがわかります.

つまり、4以下の自然数のうち、4と互いに素な自然数の個数分だけ追加されています. これはオイラーのφ関数を用いて定式化することができ、

$$ F_4 = F_3 + \phi(4) $$ と表現できます. つまり一般的に、

$$ F_n = F_{n - 1} + \phi(n) $$

が成立します. あとは、オイラーのφ関数を全ての自然数に対してあらかじめ求めておくことで、AOJの問題を解くことができます.

しかし今回の問題では、愚直にオイラーのφ関数を全ての自然数に対して求めていては、その自然数を素因数分解する必要があるので間に合いません.　そこでエラトステネスの篩の考え方を用いて求めることを考えます. (エラトステネスの篩の考え方は非常に単純なのでWikipediaを参照してください.)

エラトステネスの篩の考え方を用いたオイラーのφ関数の求め方

さて、1 \leq n \leq Nである全てのnに対して\phi(n)を求めます.

まず、n = \prod_{k = 1}^{K} p_k^{e_k}で表したとき、

$$ \phi(n) = n \prod_{k = 1}^{K}(1 - \frac{1}{p_k}) $$ が成り立ちます.

したがって、nに対して、全ての素因数について1 - \frac{1}{p} = \frac{p - 1}{p}をかけていけば良いことになります.

アルゴリズム的には以下のようになります.

  1. phi[N + 1]を用意し、phi[i] = iと初期化する.
  2. phi[i] = iのときN以下の全てのiの倍数に対して\frac{i - 1}{i}をかける.
  3. 2の処理を2からNまで繰り返す.

2の処理で全ての因子に対して\frac{p - 1}{p}をかけ合わせるという処理を実現しています. これをプログラムで表現すると以下のようになります.

for(int i = 0; i <= N ; i++) phi[i] = i;
for(int i = 2; i <= N; i++) {
    for(int j = i; j <= N; j += i) phi[j] = phi[j] / i * (i - 1);
}

これで計算量を抑えながらオイラーのφ関数の準備が整いました. あとは、F_n = F_{n - 1} + \phi(n)の処理を書いて出力すれば終わりです.

なお初期条件はF_0 = 1, F_1 = 2です.

例題の解答例

以下に全体プログラムを載せておきます.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;
// ascending order
#define vsort(v) sort(v.begin(), v.end())
// descending order
#define vsort_r(v) sort(v.begin(), v.end(), greater<int>())
#define vunique(v) unique(v.begin(), v.end())
#define mp make_pair
#define ts(x) to_string(x)
#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)
#define repm(i, a, b) for(int i = (int)a; i > (int)b; i--)
#define bit(a) bitset<8>(a)
#define des_priority_queue priority_queue<int, vector<int>, greater<int> >
typedef long long ll;
typedef pair<int, int> P;
const ll INF = 1e18;

#define MAX_V 1000000

ll MAX = 1000000;
ll dp[1000001];
ll phi[1000001];

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    rep(i, 0, MAX + 1) phi[i] = i;
    rep(i, 2, MAX + 1) {
        if(phi[i] == i) {
            for(int j = i; j <= MAX; j += i) {
                phi[j] = phi[j] / i * (i - 1);
            }
        }
    }

    dp[0] = 1;
    dp[1] = 2;
    rep(i, 2, MAX + 1) dp[i] = dp[i - 1] + phi[i];

    int t;
    cin >> t;
    rep(i, 0, t) {
        int n;
        cin >> n;
        cout << dp[n] << endl;
    }
}

C++で順列生成 next_permutation

競技プログラミング

競技プログラミングで順列を生成したくなることは良くあります.

例えば、グラフの最短経路問題のときに、訪れるべきノードが複数与えられていて、コストが最短になるような順番を求める問題の時、考えられる全順序を試してその最小を出力すればよくなります. (各ノード間の最短経路はワーシャルフロイドなどで解いていることを前提としています.)

訪れるべきノードが、「1, 3, 5」だとしたら、1 \rightarrow 3 \rightarrow 5, 1 \rightarrow 5 \rightarrow 3, 3 \rightarrow 1 \rightarrow 5, 3 \rightarrow 5 \rightarrow 1, 5 \rightarrow 1 \rightarrow 3, 5 \rightarrow 3 \rightarrow 5の全パターンを試せばよいことになります.

そんなときにC++ではnext_permutationを使います.

まず、順列の要素を配列や、vectorで与えてあげます.

ここでは、分けて説明することにします.

1. 配列を用いる場合

#include <iostream>
#include <algorithm>

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    int array[3] = {1, 3, 5};
    do {
        rep(i, 0, 3) {
            cout << array[i] << " ";
        }
        cout << endl;
    } while(next_permutation(array, array + 3));
}

出力結果は以下のようになります.

1 3 5 
1 5 3 
3 1 5 
3 5 1 
5 1 3 
5 3 1 

int array[3] = {1, 3, 5};

で順列の要素を配列として与えています. このときに注意すべき点は、この配列は昇順にソートされていなければいけないという点です.

例えば、

int array[3] = {1, 5, 3};

というふうに定義した場合、出力結果は

1 5 3 
3 1 5 
3 5 1 
5 1 3 
5 3 1

と、意図した結果が得られなくなります.

next_permutation(array, array + 3)

では、配列の範囲を与えることで、その範囲の要素の次の順列を生成してくれます.

next_permutationでは、最後の順列を生成したあとに、最初の順列を生成しようとしたときにfalseを返すので、その時点でwhile文を抜けてくれます.

順列の要素の操作はdo-while文の中で行います. (例では単純に要素を先頭から出力しています.)

2. vectorの場合

#include <iostream>
#include <vector>
#include <algorithm>

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    vector<int> v{1, 3, 5};
    do {
        rep(i, 0, 3) {
            cout << v[i] << " ";
        }
        cout << endl;
    } while(next_permutation(v.begin(), v.end()));
}

出力結果は配列のときと同じで、

1 3 5 
1 5 3 
3 1 5 
3 5 1 
5 1 3 
5 3 1

です.

プログラムを見てもわかるとおり、配列のときとほぼ変わりません.

こちらも配列の時と同様、順列の要素を昇順にソートした状態でvectorに与えないといけないことに注意する必要があります.

next_permutation(v.begin(), v.end())

でコンテナクラスの範囲を指定しています. ここも配列のときとほぼ同じです.

まとめ

next_permutationをよく忘れるので自分用の防備録として記事にしました.

配列にしろ、vectorにしろソートしなければいけないことに注意が必要です.

next_permutationは何かと便利ですね.

統計検定2級に合格するためには

資格試験

最近、統計検定2級に合格したので、勉強方法などを残していきたいと思います.

1. なんで統計検定？

私自身機械学習に興味があり、専門書などで勉強をしているのですが、統計の知識が必要になる機会が非常に多く、統計のさわりぐらいはしっかり知っておくべきだと思い、受験することにしました.

また、機械学習に限ったことではないですが、論文などを見ると、性能評価を行うときに統計的手法を用いた分析を行っていることが非常に多く、私もそのような手法を使いこなしたいと思い勉強することにしました.

2. 統計検定の概要

公式ページには、

「統計検定」とは、統計に関する知識や活用力を評価する全国統一試験

と書いてあります. その中でも、2級は大学基礎課程 (１, 2年次学部共通)で取得すべきことについて検定を行うので、学部で統計学を学んだという方やこれから使うって方はもちろん使わない方も一度受けてみてもいいかもしれません.

また、統計検定では受験方法が選べて、「紙媒体を利用した試験」と「CBT方式試験」の二つがあります. (ちなみに私が今回受験したのはCBT方式試験です.)

「紙媒体を利用した試験」では、他の試験 (例えば、情報処理試験やTOEIC) のように受験日程が決まっていて、申し込みしてから数日後に自宅に受験票が届いて、当日試験会場に足を運んで、複数人で受験する形です.

その後採点が行われ、約一か月後に結果が掲載されます.

一方、「CBT方式試験」では、日時や会場を自分で選択でき、その会場でコンピュータを用いて試験を行います. また結果も試験が終わった直後に知ることができます.

なので、とても学習計画が立てやすく、結果も早く知りたいという方には「CBT方式試験」がおすすめです.

3. 使用した参考書や問題集

私は学部の時に統計が必修授業であったため、少しの知識はありましたので、日本統計学会が出している、「統計検定2級対応 統計学基礎」をやりました.

改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎

改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎

  • 作者: 田中豊,中西寛子,姫野哲人,酒折文武,山本義郎,日本統計学会
  • 出版社/メーカー: 東京図書
  • 発売日: 2015/12/10
  • メディア: 単行本
  • この商品を含むブログを見る

数式に慣れている方や、統計に関する知識が少しある方 (仮説検定って名前ぐらいは聞いたことある程度) であればこれ一冊で対応できると思います.

この本の良いところはやはり公式で出ているところにあります. 他にも統計学の良書はたくさんあるのですが、統計検定2級に絞った勉強をしたい場合にはこれを用いるのが間違いないと思います.

（他の参考書の場合、範囲を超えてしまう（もしくは足りない）ケースがあるので）

しかし、他のブログでも言われている通り、説明が不親切な個所が多く、背景知識がない方には読み解くことが結構難しいかもしれません.

そういう時は、ネットでググってみるのがいいです. その時にお勧めなサイトが、「統計WEB」です.

統計の基礎から非常に簡潔に、多くの具体例を用いて説明してくれているので、わからない箇所はここで知識埋めするとよいと思います.

もちろん、「統計ってなに。。。」って人はこのサイトを最初から一読すると、十分な知識をつけられるようになると思います.

「統計WEB」や「統計学基礎」を一通り終えたら過去問に挑戦します.

過去問も公式が出している公式問題集を解きました.

日本統計学会公式認定 統計検定 2級 公式問題集[2015〜2017年]

日本統計学会公式認定 統計検定 2級 公式問題集[2015〜2017年]

過去問を解いていると分かるのですが、問題の構成や問われている知識は限られてくるので、過去問演習を重点的に行いました. (問題集1周と間違えたところだけで十分です.)

4. まとめ

  • 統計を少しでも知っているという人は「統計学基礎」から
  • 何も知らないという方は「統計WEB」から
  • 一通りインプットが終わったら過去問でアウトプット

統計検定準一級とかにも興味はあるんですが、２級と準一級では大きな壁があるそうですね。。。

pythonでクローリングするならSeleniumがおすすめ

その他の忘備録

機械学習などで大量のデータが必要になることは多々あります.

Wikipediaなどではdumpファイルで一括ダウンロードできるので問題は起きませんが、必ずしも自分が使いたいデータが一括でダウンロードできるとは限りません.

そんな時におすすめなのがSeleniumです!

私自身、これまで研究でBeautifulSoupを用いてクローリング、スクレイピングを行いデータ収集を行ってきました. (BeautifulSoupもものすごく便利なのでいつか記事にしたいと考えています.)

最近新たに必要になったデータを収集しようとしたのですが、BeautifulSoupだけでは難しそうなのでSeleniumを使ってみました (BeautifulSoupだけでもできるかもしれませんが、私の技量では少し難しそうでした...). そしたら、これが便利すぎてビックリしました.

Seleniumは本来はwebアプリケーションの自動テスト用のツールだそうですが、使い方は無限大です.

今回はそんな超便利なSeleniumの紹介記事です.

最後に、Seleniumに慣れるために、自動でGoogle翻訳を開き、翻訳ボタンを押し、翻訳結果をターミナルに出力するプログラムを書きましたので、そのソースコードを載せておきます.

実行結果の節でもgif画像を貼っていますが、イメージが付きやすいようにここにも載せることにします.

f:id:linearml:20181024053558g:plain

1. インストール方法

今回は、pythonとpipがすでに導入済みということを前提にして話を進めていきたいと思います. (まだ導入していないという方は、自分の使用しているos名とpipを検索クエリに入れググってみてください.)

sudo pip install selenium

これだけです.

また、seleniumを使うにはブラウザのドライバが必要になってきます. 今回はgoogle chromeを使うことを想定して話を進めていきます.

google chromeのdriverはこちらからインストールできます.

自分のosにあったdriverをインストールして適当なところに解凍してください.

2. seleniumでできること

1. ページを開く

urlを指定して、そのページを開く事ができます.

from selenium import webdriver
driver = webdriver.Chrome('./chromedriver') # インストールしたdriverのpathを指定してください. この場合カレントディレクトリにインストールしています.
url = 'https://www.google.com'
driver.get(url)

実行するとgoogleが開けると思います.

2. htmlの情報を取得

htmlの要素、要素のタグ名など様々な情報を取得する事ができます.

逆引きリファレンスがあるので自分がやりたい事に合わせて機能を追加していくといいと思います.

ここでは、その中のいくつかを紹介したいと思います.

1. id属性から要素を取得
<div id = "hoge">hoge</div>
<div id = "foo">foo</foo>

というhtmlがあったとします. この中のidがhogeのところだけを取得したい場合、

driver.find_element_by_id('hoge')

と書く事で、取得できます.

タグの中の文字列を取得したい場合は、

 driver.find_element_by_id('hoge').text

と書けばokです.

2. class属性から要素を取得
<div class = 'hoge'>hoge</hoge>
<div class = 'foo'>foo</foo>

というhtmlに対して、classがhogeのところだけを取得したい場合、

driver.find_element_by_class('hoge')

と書けばokです.

idの時と同様、タグの中の文字列は、

driver.find_element_by_class('hoge').text

で取得できます.

2. 文字を入力

テキストボックスを指定して、文字を入力する事ができます.

例えばgoogleのテキストボックスは

<input class='gsfi' id='lst-ib' ...>

となっています.

chromeの場合、F12を押すとデベロッパーツールを開く事ができ、左上の矢印を押すと、クリックしたところがhtmlのどこに相当するかがすぐにわかります. これを使って知りたいボタンやテキストボックスの属性などを調べると良いでしょう.

f:id:linearml:20181024045419g:plain

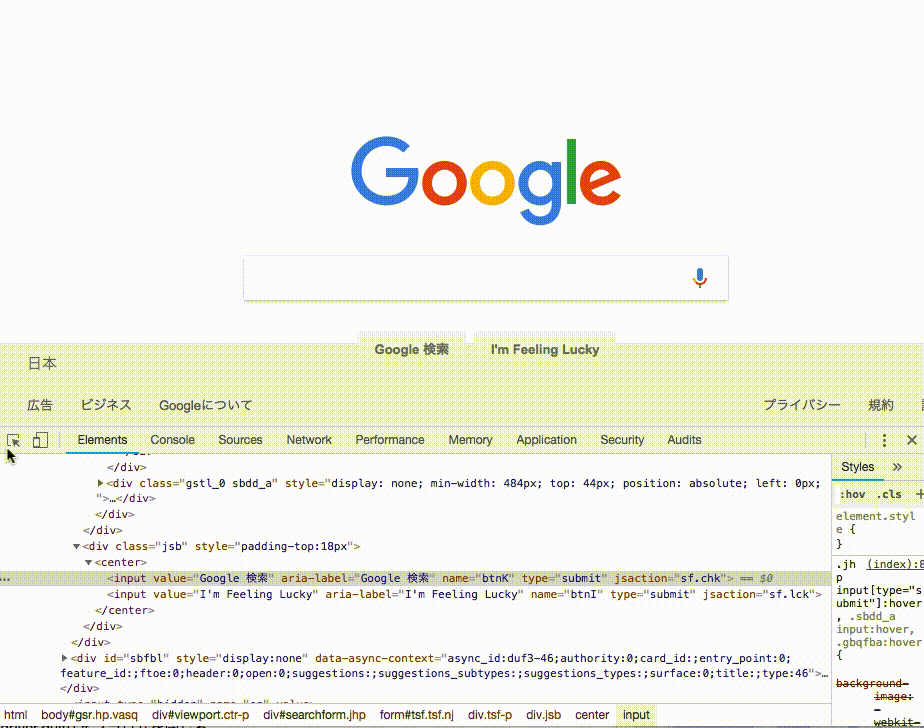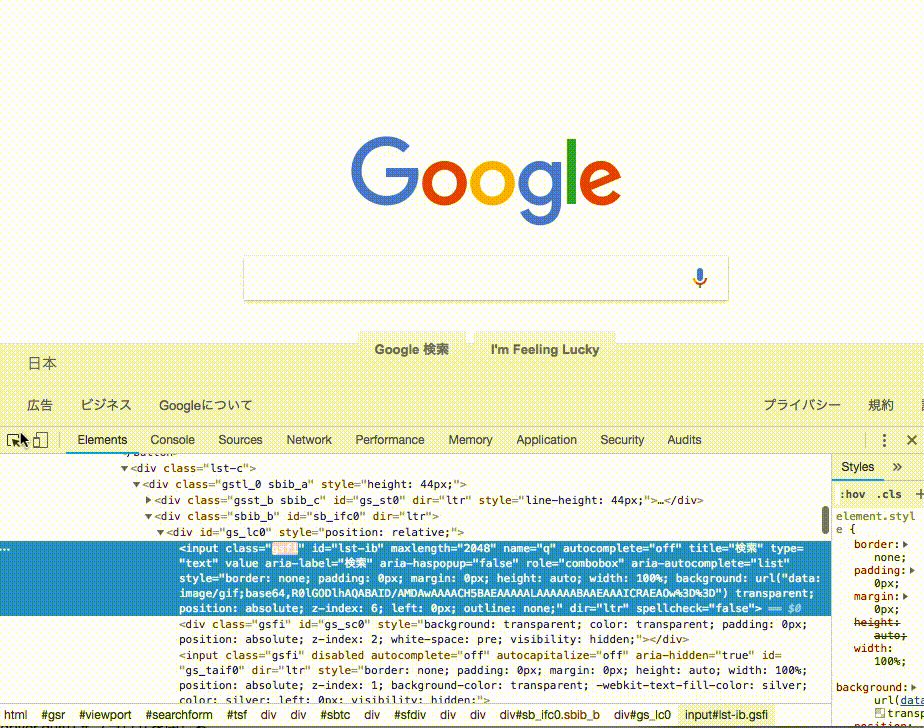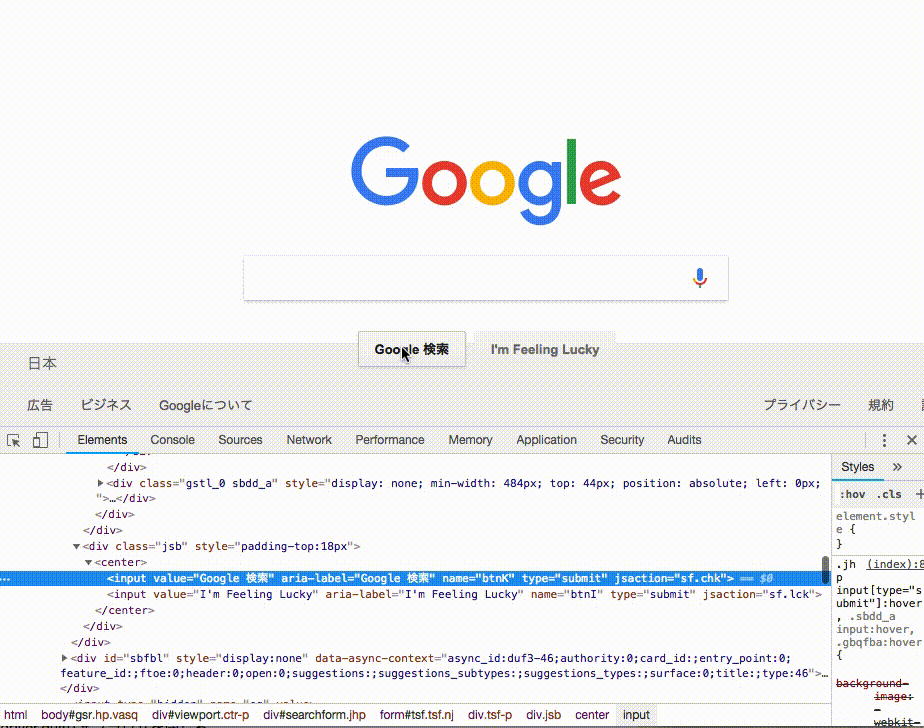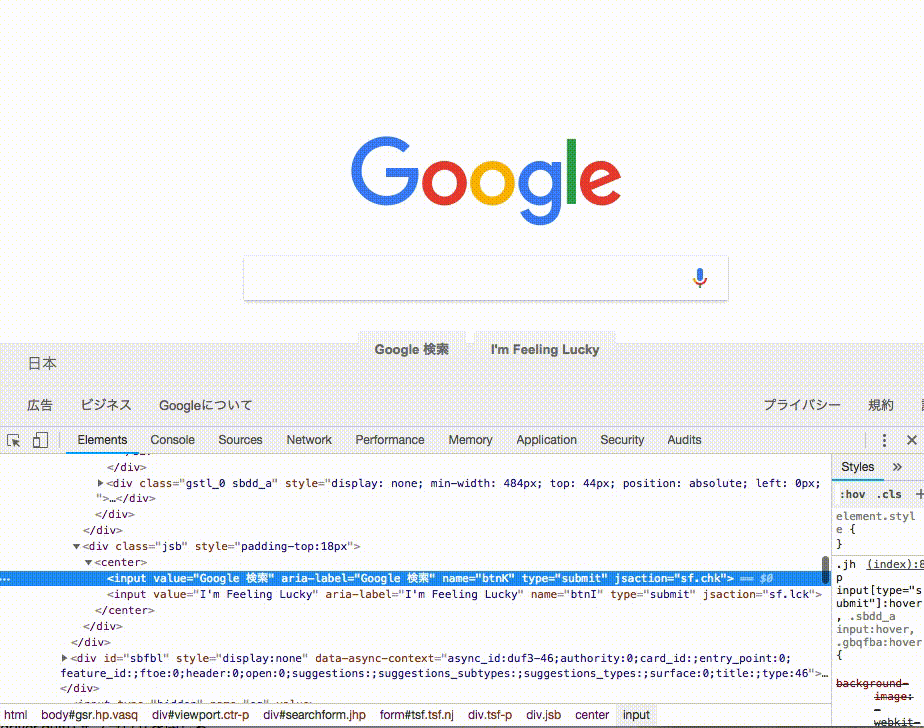
さて、今回はidを知る事ができたので、先ほどのように、テキストボックスの要素を取得します.

text_box = driver.find_element_by_id('lst-ib')

そのあとに、文字列を指定して、取得した要素に情報を送ってあげます.

text_box.send_keys('入力したい文字列')

3. ボタンをクリック

ページの好きなボタンをクリックする事ができます.

まずは、ボタンの要素を知る必要があります.

上の例のように、googleの検索ボタンの要素を調べると、

<input value="Google 検索" aria-label="Google 検索" name="btnK" ...>

となっています.

今回は、xpathを指定して要素を取得したいと思います.

xpathとは、XML中の要素や属性などを指定するための言語です.

詳しい説明はqiitaのページがとても参考になるのでこちらを読んでみてください.

さて、上のhtmlの場合、xpathは、

//input[@name='btnK']

となります. inputとその中に含まれる、属性nameについても指定してあげる事で、要素を一つに絞る事ができます.

このxpathを用いて、

button = driver.find_element_by_xpath("//input[@name='btnK']")

と書く事で、検索ボタンの要素を取得する事ができます.

このボタンをクリックするためには、

button.click()

と書けばokです.

4. ウインドウを閉じる

ウィンドウを一つ閉じたい場合は、

driver.close()

全て閉じたい場合は

driver.quit()

と書きます.

3. 実装例 : google翻訳を用いて翻訳してくれるスクリプトを作成

pythonの標準入力で英語を受け取り、seleniumを用いて、検索から翻訳結果の取得までを行うスクリプトを作成しました.

今回はリアルタイム翻訳ではなく、「翻訳」ボタンを押す事で、翻訳するようにしたいので、まず、リアルタイム翻訳を無効にします.

その後で、テキストボックスに英語を入力し、翻訳結果を取得し、ターミナルに出力しています.

1. ソースプログラム
#coding : utf-8
from selenium impot webdriver
import time

word = raw_input() # 標準入力で英語を受け取る
url = 'https://translate.google.co.jp/?hl=ja#en/ja/'

driver = webdriver.Chrome('./chromedriver')
driver.get(url)

time.sleep(3)

unvalid = driver.find_element_by_id('gt-otf-switch') # リアルタイム翻訳を無効にする
unvalid.click()

time.sleep(3)

text_box = driver.find_element_by_id('source')
text_box.send_keys(word) # テキストボックスに入力

time.sleep(3)

button = driver.find_element_by_xpath("//input[@id='gt-submit']")
button.click()  # 翻訳ボタンをクリック

time.sleep(3)

result = driver.find_element_by_id('result_box') # 翻訳結果を取得
print result.text

driver.quit() # ブラウザを閉じる

実行結果がわかりやすくなるように適宜処理を一時停止しています.

2. 実行結果

f:id:linearml:20181024053558g:plain

4. まとめ

今回は、Seleniumの紹介をしました.

Seleniumを使う事で、クローリングやwebアプリケーションの自動テストなど様々な事ができますので、これを機にマスターしてみようと思います.

numpyで集合演算をするための備忘録

その他の忘備録

研究で集合演算を使うことがあるのですが、すぐに使い方を忘れてしまうため、自分用の備忘録として記事にしたいと思います.

積集合

A \cap B

使い方

import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([2, 3, 5])

np.intersect1d(a, b)

結果

array([2, 3])

和集合

A \cup B

使い方

import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([2, 3, 5])

np.union1d(a, b)

結果

array([1, 2, 3, 4, 5])

差集合

A \backslash B

使い方

import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([2, 3, 5])

np.setdiff1d(a, b)

結果

array([1, 4])

排他的論理和

A \quad xor \quad B

使い方

import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([2, 3, 5])

np.setxor1d(a, b)

結果

array([1, 4, 5])

AtCoder Beginner Contest 112に参加しました

競技プログラミング

AtCoder Beginner Contest 112に参加したので記録を残したいと思います.

問題のタイトルは以下のようになっています.

  • A - Programming Education
  • B - Time Limit Exceeded
  • C - Pyramid
  • D - Partition

A - Programming Education

問題の概要

入力が N = 1ならば'Hello World'を出力し、N = 2ならば更に整数の入力A, Bを受け取り、A + Bの結果を出力する.

解法

N = 1のときとN = 2のときで条件分岐してあげます.

最初に整数A, Bを受け取るのではなく、 N = 2のときにのみ入力を受け取るように気をつけます.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;
// ascending order
#define vsort(v) sort(v.begin(), v.end())
// descending order
#define vsort_r(v) sort(v.begin(), v.end(), greater<int>())
#define vunique(v) unique(v.begin(), v.end())
#define mp make_pair
#define ts(x) to_string(x)
#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)
#define repm(i, a, b) for(int i = (int)a; i > (int)b; i--)
#define bit(a) bitset<8>(a)
#define des_priority_queue priority_queue<int, vector<int>, greater<int> >
#define all(v) (v).begin(), (v).end()
typedef long long ll;
typedef pair<int, int> P;
const ll INF = 1e18;

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    int N;
    cin >> N;
    if(N == 1) {
        cout << "Hello World" << endl;
    } else {
        int A, B;
        cin >> A >> B;
        cout << A + B << endl;
    }
}

B - Time Limit Exceeded

問題の概要

N個の経路のなかで、時間T以内に帰宅できる経路のうちコストが最小となる経路のコストを出力する.

ただし、i番目の経路はコストc_iかけて時間t_iで帰宅できる.

解法

全探索します. 時間T以下のt_iに対応するコストc_iの中で最小のものを出力することで目的を果たせます.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;
// ascending order
#define vsort(v) sort(v.begin(), v.end())
// descending order
#define vsort_r(v) sort(v.begin(), v.end(), greater<int>())
#define vunique(v) unique(v.begin(), v.end())
#define mp make_pair
#define ts(x) to_string(x)
#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)
#define repm(i, a, b) for(int i = (int)a; i > (int)b; i--)
#define bit(a) bitset<8>(a)
#define des_priority_queue priority_queue<int, vector<int>, greater<int> >
#define all(v) (v).begin(), (v).end()
typedef long long ll;
typedef pair<int, int> P;
const ll INF = 1e18;

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    int N, T;
    cin >> N >> T;
    vector<int> c, t;
    rep(i, 0, N) {
        int tmp_c, tmp_t;
        cin >> tmp_c >> tmp_t;
        c.push_back(tmp_c);
        t.push_back(tmp_t);
    }

    int rsl = 1e9;

    rep(i, 0, N) {
        if(t[i] <= T) rsl = min(rsl, c[i]);
    }
    if(rsl == 1e9) cout << "TLE" << endl;
    else cout << rsl << endl;

}

C - Pyramid

問題の概要

ピラミッドには中心座標(C_X, C_Y)と高さHが定まっている. 座標(X, Y)の高度はmax(H - |X - C_x| - |Y - C_Y|, 0)である.

(x_i, y_i)の高度はh_iであるという情報がN個与えられるので、その情報をもとに中心座標と高さを求める.

解法

最初はなんのこっちゃ分からなかったのですが、入力例2のC_X, C_Yが0以上100以下の整数であるとわかっていることに注意せよ.という一文を見て閃きました.

C_XとC_Yが100以下の整数ならそれらに対して全探索しちゃえば良いのでは？と考えました. (制約を見た時点で思いつくべきでしたが、なぜかこの一文を見た時に解法を思いつきました.)

そうすると、残るHをどうするかが問題になってきます. 残るHを定めてしまえば、適当に定めたC_X, C_Y, Hを用いてN個の情報に矛盾しないか一つずつ試していけば良いことになります.

Hの定め方はh_0が0のときとそうでないときで場合分けしました.

  • h_0が0でないとき

    max(H - |X - C_X| - |Y - C_Y|, 0)という定義より、ある中心座標の候補であるC^{\prime}_{X}, C^{\prime}_{Y}を用いて、h_0 = H^{\prime} - |x_0 - C^{\prime}_{X}| - |y_0 - C^{\prime}_Y|が成り立ちます. したがって、H^{\prime} = h_0 + |x_0 - C^{\prime}_X| + |y_0 - C^{\prime}_Y|となります.

    これで、あるC^{\prime}_{X}, C^{\prime}_{Y}に対するH^{\prime}を一つ定めることができました. このH^{\prime}を用いたとき全ての情報に矛盾が生じなかったとき、そのC^{\prime}_{X}, C^{\prime}_Y, H^{\prime}が答えとなります.

  • h_0が0のとき

    h_0が0のときは、H^{\prime} - |x_0 - C^{\prime}_{X}| - |y_0 - C^{\prime}_{Y}| \leq 0となります. したがって、H^{\prime}の値は、1 \leq H^{\prime} \leq |x_0 - C^{\prime}_{X}| + |y_0 - C^{\prime}_{Y}|に絞ることができます. したがってこの範囲の中で情報に矛盾の生じないH^{\prime}が存在すれば、そのC^{\prime}_{X}, C^{\prime}_Y, H^{\prime}が答えとなります.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;
// ascending order
#define vsort(v) sort(v.begin(), v.end())
// descending order
#define vsort_r(v) sort(v.begin(), v.end(), greater<int>())
#define vunique(v) unique(v.begin(), v.end())
#define mp make_pair
#define ts(x) to_string(x)
#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)
#define repm(i, a, b) for(int i = (int)a; i > (int)b; i--)
#define bit(a) bitset<8>(a)
#define des_priority_queue priority_queue<int, vector<int>, greater<int> >
#define all(v) (v).begin(), (v).end()
typedef long long ll;
typedef pair<int, int> P;
const ll INF = 1e18;

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    int N;
    cin >> N;
    vector<int> x, y, h;
    rep(i, 0, N) {
        int tmp_x, tmp_y, tmp_h;
        cin >> tmp_x >> tmp_y >> tmp_h;
        x.push_back(tmp_x);
        y.push_back(tmp_y);
        h.push_back(tmp_h);
    }

        rep(xi, 0, 101) rep(yi, 0, 101) {
            if(h[0] != 0) {
                int H = h[0] + abs(x[0] - xi) + abs(y[0] - yi);
                bool flag = true;
                rep(i, 0, N) {
                    if(h[i] != max(H - abs(x[i] - xi) - abs(y[i] - yi), 0)) {
                        flag = false;
                        break;
                    }
                }
                if(flag) {
                    cout << xi << " " << yi << " " << H << endl;
                    return 0;
                }
            } else {
                int max_h = abs(x[0] - xi) + abs(y[0] - yi);
                rep(hi, 0, max_h + 1) {
                    bool flag = true;
                    rep(i, 0, N) {
                        if(h[i] != max(hi - abs(x[i] - xi) - abs(y[i] - yi), 0)) {
                            flag = false;
                            break;
                        }
                    }
                    if(flag) {
                        cout << xi << " " << yi << " " << hi << endl;
                    }
                }
            }
        }
}

D - Partition

問題の概要

整数N, Mが与えられる.

\sum_{i = 1}^{N} a_{i} = Mとなる整数からなる長さNの数列aにおいて、a_1, a_2, \cdots, a_Nの最大公約数の取り得る最大値を求める.

解法

整数問題苦手ですね... またしても時間内に解けませんでした.

例えば数列aの最大公約数をdとしたとき、a_i, (i = 1, 2, \cdots, N)はdの倍数となります. したがって、それらの和であるMもdの倍数となります.

Mがdの倍数、つまりdはMの約数であることに注意すると、dの候補を全部列挙することができます. (約数を列挙するライブラリを持っていると便利です.)

a_1, a_2, \cdots, a_N \geq dであることに注意すると、M \geq N \times dとなります.

M \geq N \times dを満たすdを用いて、a_1 = a_2 = \cdots = a_{N - 1} = d、a_N = M - (N - 1) \times dとすることで、最大公約数がdとなる数列aを作ることができます.

したがって、Mの約数でありかつ、M \geq N \times dを満たすdの中の最大値を結果として出力してあげれば良いことになります.

#include <iostream>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <set>
#include <cstring>

using namespace std;
// ascending order
#define vsort(v) sort(v.begin(), v.end())
// descending order
#define vsort_r(v) sort(v.begin(), v.end(), greater<int>())
#define vunique(v) unique(v.begin(), v.end())
#define mp make_pair
#define ts(x) to_string(x)
#define rep(i, a, b) for(int i = (int)a; i < (int)b; i++)
#define repm(i, a, b) for(int i = (int)a; i > (int)b; i--)
#define bit(a) bitset<8>(a)
#define des_priority_queue priority_queue<int, vector<int>, greater<int> >
#define all(v) (v).begin(), (v).end()
typedef long long ll;
typedef pair<int, int> P;
const ll INF = 1e18;

vector<ll> divisor(ll n) {
    vector<ll> res;
    for(int i = 1; i * i <= n; i++) {
        if(n % i == 0) {
            res.push_back(i);
            if(i != n / i) res.push_back(n / i);
        }
    }
    return res;
}

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    ll N, M;
    cin >> N >> M;

    vector<ll> v = divisor(M);
    ll max_v = 1;

    rep(i, 0, v.size()) {
        if(v[i] * N <= M) max_v = max(max_v, v[i]);
    }
    
    cout << max_v << endl;
}

感想

C問題に関しては制約を見逃すことが多く、4WA1ACという結果でした...

ここら辺の正確性をどうにかすればもう少し良いレートになれるかなと感じています.

また、整数問題もリアルタイムで解けることが少ないので、練習していく必要がありますね...